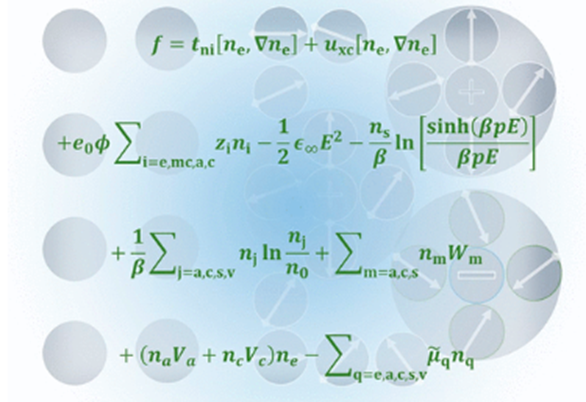
A hybrid density–potential functional of an electrochemical interface that encompasses major effects in the contacting metal and electrolyte phases is formulated. Variational analysis of this functional yields a grand-canonical model of the electrochemical double layer (EDL). Specifically, metal electrons are described using the Thomas–Fermi–Dirac–Wigner theory of an inhomogeneous electron gas. The electrolyte solution is treated classically at the mean-field level, taking into account electrostatic interactions, ion size effects, and nonlinear solvent polarization. The model uses parametrizable force relations to describe the short-range forces between metal cationic cores, metal electrons, and electrolyte ions and solvent molecules. Therefore, the gap between the metal skeleton and the electrolyte solution, key to properties of the EDL, varies consistently as a function of the electrode potential. Partial charge transfer in the presence of ion specific adsorption is described using an Anderson–Newns type theory. This model is parametrized with density functional theory calculations, compared with experimental data, and then employed to unravel several interfacial properties of fundamental significance in electrochemistry. In particular, a closer approach of the solution phase toward the metal surface, for example, caused by a stronger ion specific adsorption, decreases the potential of zero charge and elevates the double-layer capacitance curve. In addition, the ion specific adsorption can lead to surface depolarization of ions. The present model represents a viable framework to model (reactive) EDLs under the constant potential condition, which can be used to understand multifaceted EDL effects in electrocatalysis.

https://doi.org/10.1021/acs.jctc.1c00098